本文讨论如何在LTspice仿真中利用flat()、gauss()和mc()函数来实现伪随机数和真随机数的生成,并介绍如何使用设置面板的Hacks部分中的Use the clock to reseed the MC generator(使用时钟重新设置MC生成器的随机种子)选项。文章探讨了伪随机数和真随机数之间的利弊权衡,同时比较了蒙特卡罗统计仿真与更有针对性的最坏情况仿真之间的差异。
在LTspice原理图中,有多种方法可模拟随机性。LTspice中的flat()、gauss()和mc()函数支持在LTspice仿真中引入随机性。本文以mc()函数为例,说明如何模拟无源元件值的容差。打开LTspice 后,选择Help > LTspice Help(“帮助”>“LTspice帮助”,或按F1)可打开《帮助手册》,了解有关flat()和gauss()的更多信息。
图1中的示例使用mc()来设置R1和C1的标称值和容差。例如,R1的标称值为10 kΩ,容差为5%。mc(x,y)函数将生成在x*(1-y)和x*(1+y)之间均匀分布的伪随机数。请继续阅读,深入了解伪随机数和真随机数之间的区别,以及如何强制LTspice生成真随机数。.STEP指令用于指示LTspice运行仿真的迭代次数。在下面的示例中,.STEP指令以1为增量将一个虚拟参数从1逐步增加到100,从而进行100 次仿真运行,其中R1和C1的值都是随机生成。
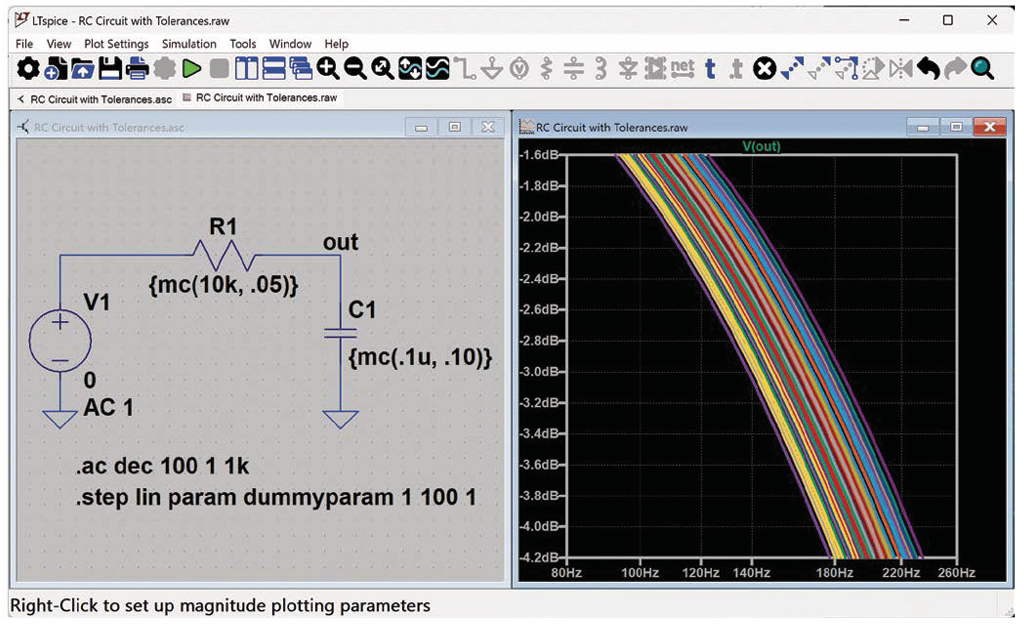
图1. RC电路使用mc()来设置无源元件的值和容差
观察mc()函数在每一步迭代中的行为:图2显示了一个仅使用电压源的简单示例。此示例使用mc()将标称电压设置为10 V,并将容差设置为100%。因此,预计将得到一个在0 V和20 V之间均匀分布的电压。从波形查看器和SPICE输出日志中的结果可以看到,在10次迭代中,电压变化范围是2.7 V至19.92 V,分布并不完全均匀,但更多次迭代将有助于确保结果在统计上更加合理。
图2. 电压源使用mc()生成随机电压
我们不妨更仔细地观察,并反复运行这个仿真。在这些仿真过程中,数值是否发生了变化?在我的计算机上,每次运行仿真时,每一步迭代都得到相同的电压值。这称得上“随机”吗?
您所看到的是代码和计算机在生成随机数时的典型表现。编程语言中的随机数生成器有一个与之关联的可选seed()方法。想要获得真随机数(即每次运行程序时得到不同的随机数),需要调用seed()方法,并为其指定动态变化的种子值。通常,程序员会将当前系统时间传递给seed()方法来实现这种随机性。
这与我们的LTspice仿真有何关系?如果希望每次运行仿真时获得不同的随机值,则必须在设置面板的Hacks部分中启用Use the clock to reseed the MC generator选项(参见图3)。
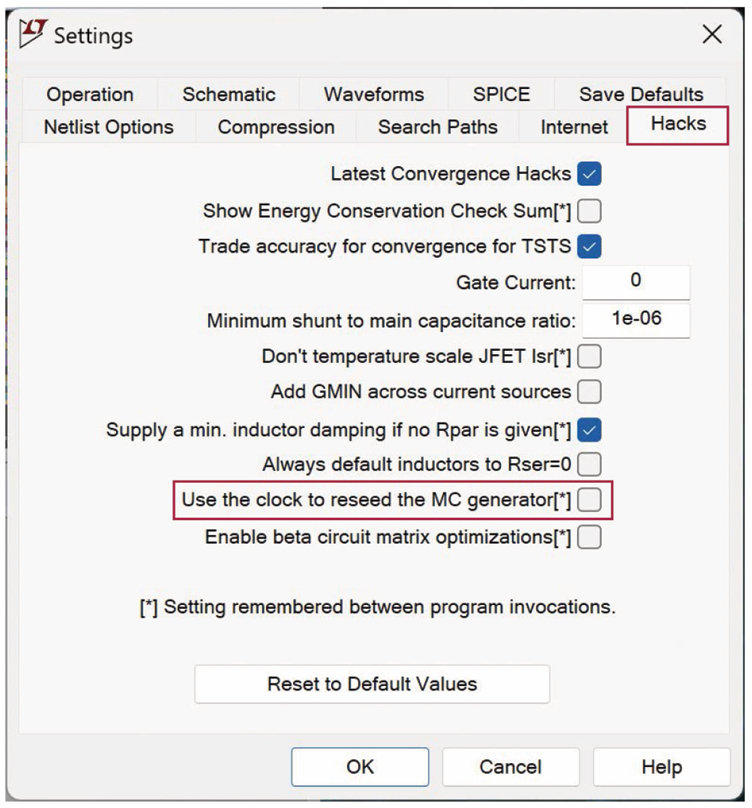
图3. LTspice设置面板的Hacks选项卡,显示了如何实现真随机性
此Use the clock to reseed the MC generator选项也适用于flat()和gauss()函数。这些函数可以用在mc()所使用的地方。
不过,请慎重考虑否是需要刻意实现这种仿真行为。您希望仿真过程是真随机的吗?倘若如此,您的仿真将失去可预测性和可重复性。
为了说明这一点,让我们回顾图2中的示例。如果目标是模拟一个在0 V和20 V之间均匀分布的电压呢?当前的示例不太符合预期。然而,通过将迭代次数从10次增加到100次,我们可以使仿真结果更接近目标(图4)。这种调整使得仿真更接近实现预期的分布范围。
图4. 使用mc()且迭代更多次数的电压源
现在有两点已经很明确:(a)mc()迭代运行100次,便能得到一个相当好的数值分布;(b)如果不启用reseed the MC generator(重新设置MC生成器的随机种子)功能,则每次运行仿真将得到可重复的结果。
如果电路中多处使用mc()呢?能否保证通过100次迭代能够覆盖所有容差?图5展现了这一尝试,其中显示了两个使用mc()的电压源。将V(out1)作为y轴、V(out2)作为x轴进行绘图,可以清楚地看到,V1和V2的组合呈现出高度随机的坐标分布(右键单击x轴标题,将x轴从步进虚拟参数更改为V(out2))。但从技术上讲,这些电压的最小值和最大值并非同时达到,导致极端(角落)情况的覆盖有些不足。
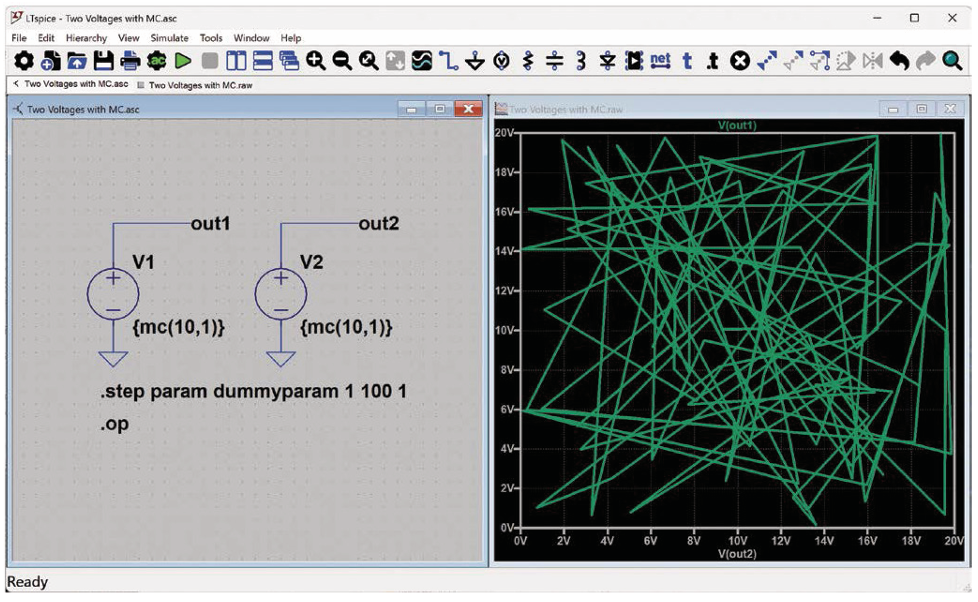
图5. 绘制一次仿真中两个mc()电压的结果
如果目标是接近完全覆盖,则需要更多次迭代(图6)。
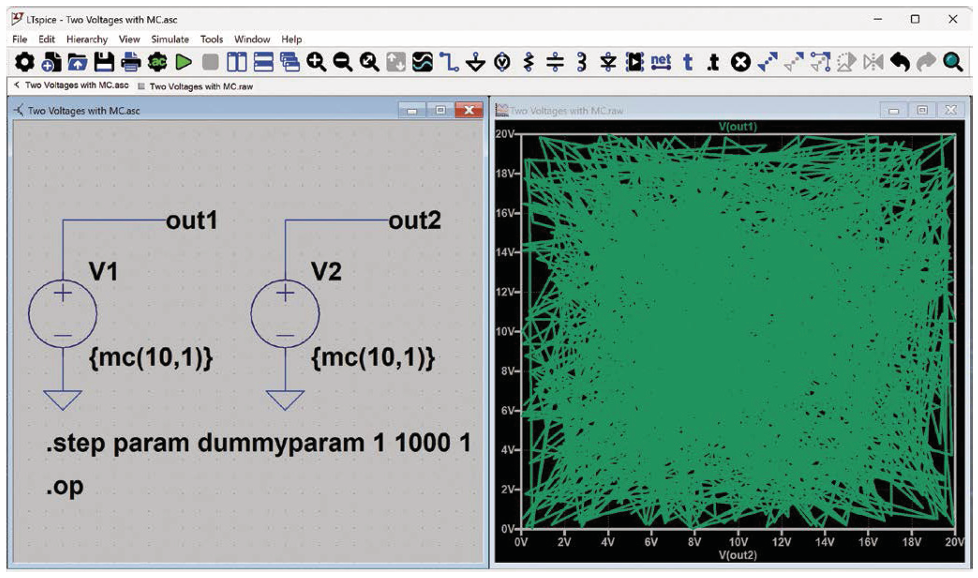
图6. 绘制更多次迭代的结果
对于这个简单的例子,仿真运行速度相当快,即便运行1000次也毫无问题。但如果仿真运行时间很长,运行多次迭代需要数小时或数天时间呢?应考虑启用Use the clock to reseed the MC generator选项是否有帮助。如果在一次仿真运行中,mc()生成的值令人满意,那么接下来的目标是让这些结果在每次运行时可重复,还是随机变化呢?启用此项功能之前,这是一个值得考虑的好问题。
为了大幅缩短仿真时间,我们来看一种相对不太随机的方法。
图7所示的例子确保了仿真能够覆盖无源元件容差的所有边缘情况,同时保持总体仿真时间尽可能短。这个例子遍历了R1的三个值和C1的三个值,进行了九次仿真,并覆盖了元件值同时达到最小值(或最大值)的情形。
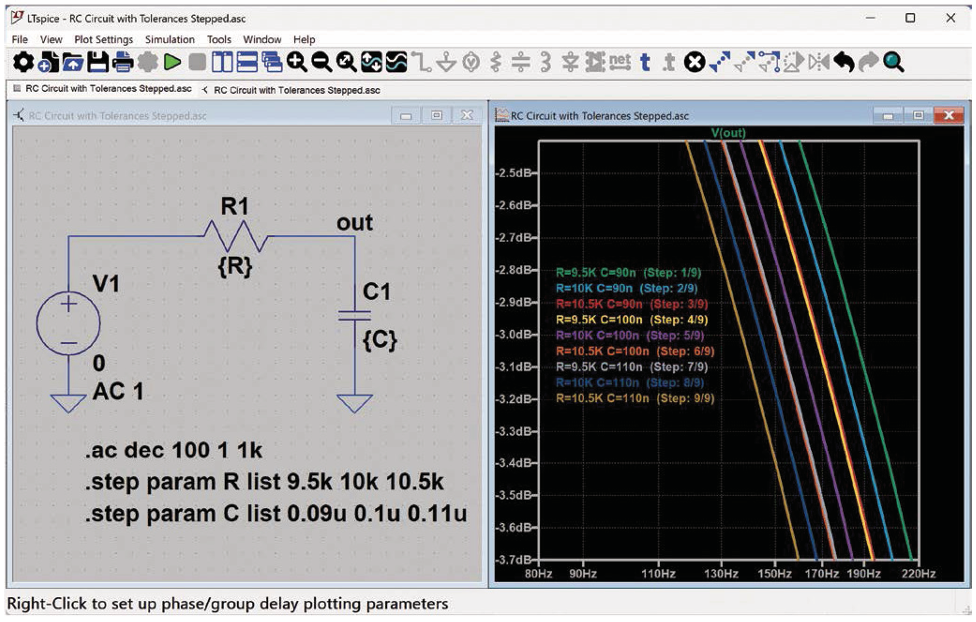
图7. 设置元件的特定值以模拟容差导致的行为
如果目标是探索电路在极端工况下的行为,则相对不太随机的方法可能更为合适。相反,如果目标是对仿真在一系列变化下的行为进行统计分析,则使用大量仿真并通过随机函数引入随机性可能是更好的方法。但无论哪种情况,您现在应该已经对如何在LTspice仿真中引入(或不引入)随机性有了更好的理解。